| カックロ ルールと解き方Rules and how to solve Kakuro. |
ルール
Rules
- 次の条件に合うように空いている白枡に1~9の数字を入れます。 Fill the empty white cells with numbers 1 to 9 to meet the following conditions.
- 問題枡(黒枡)の下に連続した解答枡(白枡)にはそれぞれ1~9の数字が1回ずつ入り、その合計が問題枡の斜線左下の数値になります。 The numbers 1 to 9 are entered once in each of the answer cells (white cells) that are continuous to the below of the problem cell (black cell), and the total is the number in the lower left corner of the problem cell.
- 問題枡(黒枡)の右に連続した解答枡(白枡)にはそれぞれ1~9の数字が1回ずつ入り、その合計が問題枡の斜線右上の数値になります。 The numbers 1 to 9 are entered once in each of the answer cells (white cells) that are continuous to the right of the problem cell (black cell), and the total is the number in the upper right corner of the problem cell.
かっくろの問題へ jump to Kakuro problem.
解くコツ
Tips for solving
解くポイントは解答枡の連続数毎に組み合わせが一意に決まる合計値(問題数値)が有りますのでこのようなところから注目していきます。その例は 二枡連続の解答枡で合計(問題数値)が3なら入る数字の組み合わせは1と2です。四枡連続で合計が11なら1,2,3,5という組み合わせになります。
このように一意に決まる組み合わせは次の通りです。 The points to be solved have a total value (problem number) for which the combination is uniquely determined for each continuous number of answer cells.
For example, if the total (question number) is 3 for two consecutive answer cells, the combination of numbers that can be entered is 1 and 2. If the total is 11 for four consecutive answer cells, it will be a combination of 1, 2, 3, and 5 .
The combination that is uniquely determined in this way is below.
| 連続枡数Number of continuous cells | 合計値Total value | 数字の組み合わせCombination of numbers | 連続枡数Number of continuous cells | 合計値Total value | 数字の組み合わせCombination of numbers | 連続枡数Number of continuous cells | 合計値Total value | 数字の組み合わせCombination of numbers | 連続枡数Number of continuous cells | 合計値Total value | 数字の組み合わせCombination of numbers |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 1,2 | 2 | 4 | 1,3 | 2 | 16 | 7,9 | 2 | 17 | 8,9 |
| 3 | 6 | 1,2,3 | 3 | 7 | 1,2,4 | 3 | 23 | 6,8,9 | 3 | 24 | 7,8,9 |
| 4 | 10 | 1,2,3,4 | 4 | 11 | 1,2,3,5 | 4 | 29 | 5,7,8,9 | 4 | 30 | 6,7,8,9 |
| 5 | 15 | 1,2,3,4,5 | 5 | 16 | 1,2,3,4,6 | 5 | 34 | 4,6,7,8,9 | 5 | 35 | 5,6,7,8,9 |
| 6 | 21 | 1,2,3,4,5,6 | 6 | 22 | 1,2,3,4,5,7 | 6 | 38 | 3,5,6,7,8,9 | 6 | 39 | 4,5,6,7,8,9 |
| 7 | 28 | 1,2,3,4,5,6,7 | 7 | 29 | 1,2,3,4,5,6,8 | 7 | 41 | 2,4,5,6,7,8,9 | 7 | 42 | 3,4,5,6,7,8,9 |
| 8 | 36 | 1,2,3,4,5,6,7,8 | 8 | 37 | 1,2,3,4,5,6,7,9 | 8 | 38 | 1,2,3,4,5,6,8,9 | 8 | 39 | 1,2,3,4,5,7,8,9 |
| 8 | 40 | 1,2,3,4,6,7,8,9 | 8 | 41 | 1,2,3,5,6,7,8,9 | 8 | 42 | 1,2,4,5,6,7,8,9 | 8 | 43 | 1,3,4,5,6,7,8,9 |
| 8 | 44 | 2,3,4,5,6,7,8,9 | 9 | 45 | 1,2,3,4,5,6,7,8,9 | ||||||
| 連続枡数Number of continuous cells | 合計値Total value | 数字の組み合わせCombination of numbers | 連続枡数Number of continuous cells | 合計値Total value | 数字の組み合わせCombination of numbers |
|---|---|---|---|---|---|
| 2 | 3 | 1,2 | 2 | 4 | 1,3 |
| 2 | 16 | 7,9 | 2 | 17 | 8,9 |
| 3 | 6 | 1,2,3 | 3 | 7 | 1,2,4 |
| 3 | 23 | 6,8,9 | 3 | 24 | 7,8,9 |
| 4 | 10 | 1,2,3,4 | 4 | 11 | 1,2,3,5 |
| 4 | 29 | 5,7,8,9 | 4 | 30 | 6,7,8,9 |
| 5 | 15 | 1,2,3,4,5 | 5 | 16 | 1,2,3,4,6 |
| 5 | 34 | 4,6,7,8,9 | 5 | 35 | 5,6,7,8,9 |
| 6 | 21 | 1,2,3,4,5,6 | 6 | 22 | 1,2,3,4,5,7 |
| 6 | 38 | 3,5,6,7,8,9 | 6 | 39 | 4,5,6,7,8,9 |
| 7 | 28 | 1,2,3,4,5,6,7 | 7 | 29 | 1,2,3,4,5,6,8 |
| 7 | 41 | 2,4,5,6,7,8,9 | 7 | 42 | 3,4,5,6,7,8,9 |
| 8 | 36 | 1,2,3,4,5,6,7,8 | 8 | 37 | 1,2,3,4,5,6,7,9 |
| 8 | 38 | 1,2,3,4,5,6,8,9 | 8 | 39 | 1,2,3,4,5,7,8,9 |
| 8 | 40 | 1,2,3,4,6,7,8,9 | 8 | 41 | 1,2,3,5,6,7,8,9 |
| 8 | 42 | 1,2,4,5,6,7,8,9 | 8 | 43 | 1,3,4,5,6,7,8,9 |
| 8 | 44 | 2,3,4,5,6,7,8,9 | 9 | 45 | 1,2,3,4,5,6,7,8,9 |
数字が決まるとその枡を含む縦横に連続した白枡(解答枡)にはこの数字は入りません。同じ行か列の他の交差点に注目していきます。
それでは例題で説明します。 The point where the unique combinations cross vertically and horizontally is the point of interest. If there is only one number that fits in both the vertical and horizontal directions, the number that fits in the cell is determined.
Once the number is determined, this number will not be included in the white cells that are continuous vertically and horizontally . Look at other intersections in the same row or column.
Let's explain with an example.
| 次の図が問題です。解答枡の連続が二つのところで問題数値が3,4,16,17のところは数字の組み合わせが 決まる(3なら1と2など)ことを思い出してください。 The following figure is the problem. Remember that when there are two consecutive answer cells and the problem value is 3,4,16,17, the combination of numbers is determined. |
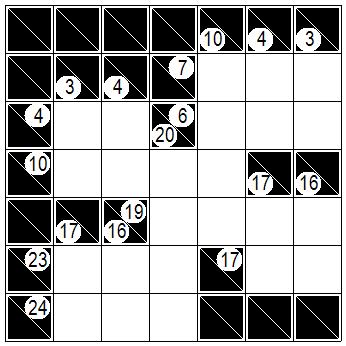
|
|
まず黄色の枡に注目してください。 一番左側で上から3枡目の問題数字4はその右に連続する二つの解答枡に入る数字の合計を表しています。この二つの枡に入る数字の組み合わせは1と3しかありません。 また上から2段目、左から二つ目の問題枡の3はその下に連続する二つの解答枡に入る数字の合計を表しています。この二つの枡に入る数字の組み合わせは1と2しかありません。 縦横連続した解答枡の交点で共通に入る数字が一つしかなければ交点の枡に入る数字は共通に入る数字に決まりますので、上から3番目左から2番目の解答枡には両方に共通な1が入ります。すると、2,3も決まります。 同じ様にして右下の水色の枡の部分も決まります。 First, pay attention to the yellow cells. The problem number 4 in the third cell from the top on the left-hand side represents the sum of the numbers in the two consecutive answer cells to the right.There are only 1 and 3 combinations of numbers in these two cells. In the second row from the top and the second row from the left, the number 3 represents the sum of the numbers in the two answer cells below.There are only 1 and 2 combinations of numbers in these two cells. If there is only one number that is common to the intersections of vertical and horizontal answer cells, the number that enters the intersection cell will be the number that will be common.So the third answer cell from the left and the second answer cell from the left contains 1 that is common to both. Then, 2 and 3 are decided. In the same way, the light blue cells at the lower right is also determined. |
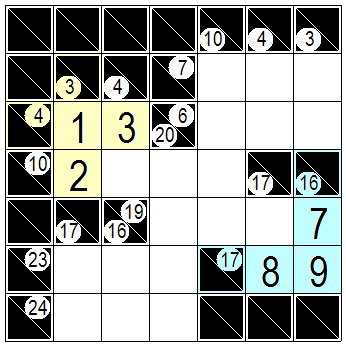
|
|
今度は右上の緑色の枡に注目します。横に3枡並んで合計が7になる組み合わせは1,2,4だけ、縦2枡並んで合計が4の組み合わせは1,3ですので交点には1しか入りません。
縦の残りの枡は3に決まります。 左下の紫色の枡も同じ様に横3枡で23なら6,8,9の組み合わせで、縦2枡の合計が16なら7,9の組み合わせのみですので交点は9に決まります。9の下は7に決まります。 Now look at the green cells in the upper right corner. There are only 1,2,4 combinations where 3 cells are arranged side by side and the total is 7. Combinations where 2 cells are arranged vertically and total is 4 are 1 and 3, so only 1 can be entered at the intersection. The remaining vertical cell is determined to be 3. In the same manner, the purple framed cells that are horizontal and total is 23 at the lower left is combination of 6, 8, 9 .And if there is 16 in the total of 2 vertical cells, there is only a combination of 7,9, so the intersection is determined to 9. Below 9 is determined to be 7. |
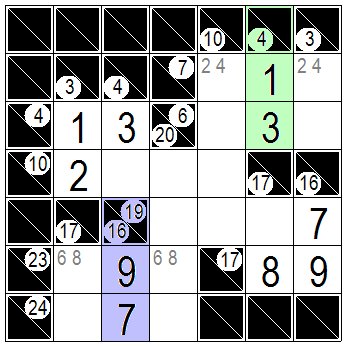
|
|
右上の緑色の問題数字7⃣の右に並ぶ枡で 問題数字⑩③の下の枡には残りの2か4が入りますが 問題数字③の下の枡には 2か1しか入れませんので2になります。⑩の下は4になります。 左下の紫の23の問題枡の右に並ぶ枡でも同じように8と6が決まります。 In the cell on the right of the green problem number 7 on the upper right, the remaining 2 or 4 will be placed in the cell below the problem number 3,10 but only 2 or 1 will be inserted in the cell below the problem number 3. So this cell becomes 2.Below 10 is 4. 8 and 6 are determined in the same way even for the cells that are lined up to the right of the purple 23 problem cells in the lower left. |
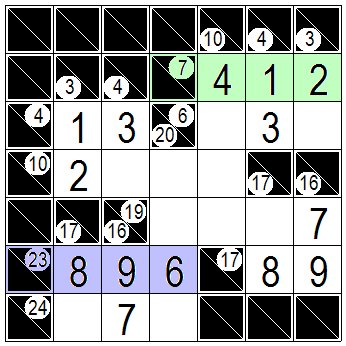
|
|
連続した解答枡で数字が決まっていないところが1箇所なら、問題で指定された合計の値からすでに決まった数字を引いていけば直ぐに決められます。 緑色の枡の1、黄色の枡の1、紫の枡の9、水色の枡の9が枡が直ぐに決まり次図になります。 If there is only one place where numbers are not determined in consecutive answer cells, you can determine them immediately by subtracting the numbers already determined from the total value specified in the problem. The green cell 1, the yellow cell 1, the purple cell 9 and the light blue cell 9 are determined immediately, as shown in the following figure. |
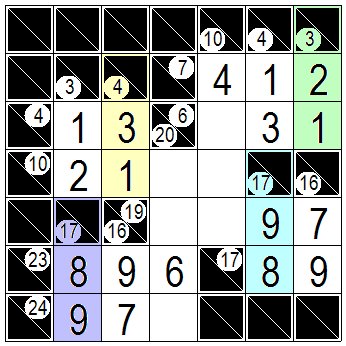
|
|
上と同じように連続した解答枡で1枡だけ数字が決まっていない、緑色の枠の枡の数字2が決まります。 また黄色の解答枡の位置に注目すると横の連続は4枡で合計が10、同じく縦も連続が4枡で合計が10ですので1,2,3,4の組み合わせになります。ところが1と2は横の連続枡に既に入っており、 4は縦の連続枡に既に入っています。するとこの交点の黄色の枡には残った3しか入れません。 In the same way as above, the number 2 is determined for the green cell, where the number is not determined for only one cell in the continuous answer cell. Also, paying attention to the position of the yellow answer cell, the horizontal continuation is 4 cells and the total is 10, and the vertical continuation is also 4 cells and the total is 10, so it is a combination of 1,2,3,4. However, 1 and 2 are already in the horizontal continuous cells, 4 is already in the vertical continuous cells.Then, only the remaining 3 can be put in the yellow cell at this intersection. |
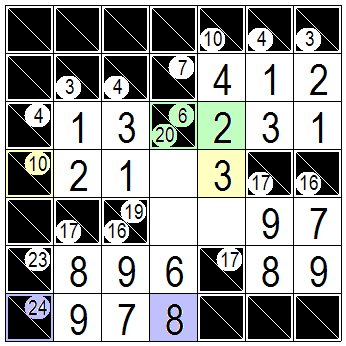
|
|
連続した解答枡で数字が入らずに残っている枡が一つの黄色の枡が4に、水色の枡は1に決まります。 A yellow cell that is a continuous answer cell with only one cell left without a number becomes 4,light blue cell becomes 1. |
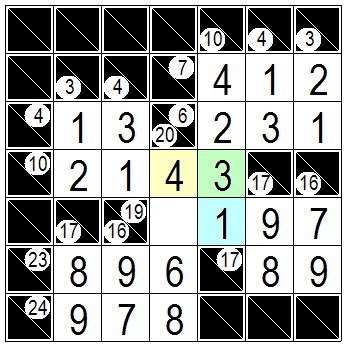
|
|
最後に残った枡が2となり これが正解になります。 ここでは基本的な手筋しか出てきませんでしたが、まだまだいろいろな手筋があります。 カックロでは「ある枡にいくつが入ったとして・・・」というような仮定をすることは有りません。(仮定をしなくても解けるのがニコリの標準です) The last remaining cell is 2, which is the correct solution. Here, only the basic steps came out, but there are still many other steps. Kakuro does not make assumptions such as "If this cell becomes 1,then...". (Nikoli's standard is that it can be solved without making assumptions) |

|
|
次に他の手筋 解くポイント、コツをいくつか説明します。 次の図を見てください。問題の一部ですが 右側のピンクの問題枡8は 下に縦3枡の解答枡があります。3枡で8になるのは 1,2,5と1,3,4の二通りです。 また黄色の問題枡22は 右に横3枡の解答枡があります。3枡で22になるのは5,8,9と6,7,9の二通りです。 この縦3枡、横3枡に入る数字で共通するのは5で縦横交点の枡には5が入ります。 問題数字の合計となる数字の組み合わせが二通りになるところも注目です。 次に左側の緑の問題枡7は2桝の合計ですが2枡で7になるのは1,6と2,5と3,4の組み合わせしかありません。 また紫色の問題枡15も2枡の合計で2枡で15になる組み合わせは6,9と7,8です。縦横の交点の枡には共通した6が入ります。 Next, I will explain some other points and tips. See the following figure. It is a part of the problem, but the pink problem cell 8 on the right side has 3 vertical answer cells below this 8. There are two ways to get 8 in 3 cells: 1,2,5 and 1,3,4. In addition, the yellow problem cell 22 has 3 answer cells on the right. There are two ways of 5,8,9 and 6,7,9 to become 22 in 3 cells.The number common to the three vertical and three horizontal cell is 5, and the cell at the vertical and horizontal intersection is 5. It is also noteworthy that there are two combinations of numbers that are the sum of the problem numbers. Next, the green problem cell 7 on the left is the sum of the two cells, but there are only combinations of 1-6,2-5 and 3-4 that can be 7 in two cells.Also, there are 6,9 and 7,8 combinations of purple problem cell 15 which is 15 in 2 cells. The common 6 is placed in the cells at the intersections in the vertical and horizontal directions. |
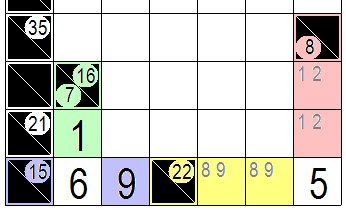
|
|
次の図を見てください。問題の一部ですが 緑色と黄色の問題枡は何れも縦2枡の合計が3で1と2が答え数字の候補になります。 ここでピンクの問題数字21の横一列の6枡に注目します。黄色と緑の枡には1か2のどちらかが入りますので残りの4枡には1と2は入れられません。 その結果 水色の枡には1か3のうち3が、紫色の枡には1,2,4のうち4が入ることになります。 See the following figure.It is a part of the problem, but both green and yellow problem cells are arranged verticaly and have total naumber is 3 , so 1 and 2 are candidate of the answer numbers. Here, pay attention to the 6 cells in a row beside the pink problem number 21. Either 1 or 2 can be entered in the yellow and green cells, so 1 and 2 cannot be entered in the remaining 4 cells. As a result, 3 out of 1 or 3 will be in the light blue cell, and 4 out of 1, 2, and 4 will be in the purple cell. |
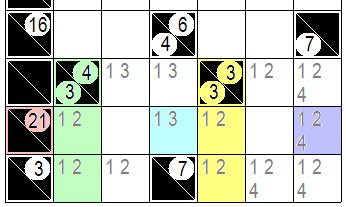
|
|
この結果 次の図のように決まります。 連続した解答枡の2か所に入る可能性のある数字が同じ数字2文字の組み合わせに決まれば 残りの枡にこれらの数字は入れられません。 この考え方を拡張すれば3数字の組み合わせが3か所で決まっていれば残りの枡にはこの3数字は入れられません。 This result is determined as shown in the following figure. If the numbers that are likely to fit in two places in a series of answer cells are determined to be a combination of the same two numbers, these numbers cannot be entered in the remaining cells. If this idea is extended, if the combination of three numbers is determined in three places, the remaining cells cannot contain these three numbers. |
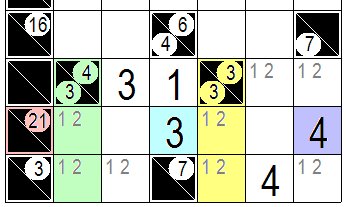
|
2020.2.28修正
2010.6.12作成
鴈野さんちのHomePage Top.
ご感想などは鴈野 敏生 まで。 2020.2.28 Modified
2010.6.12 First edition
Jump to top of Karino's HomePage.
mail to T.Karino