| 橋をかけろ(Bridge) ルールと解き方Rules and how to solve Bridge. |
ルール
Rules
- 次の条件に合うよう丸付き数字の橋脚間に橋を架けていきます。 Build a bridge between the circled piers to meet the following conditions.
- ○の中の数字はその橋脚に架ける橋の数です。 The number in ○ is the number of bridges that can be bridged on the pier.
- 橋は上下左右の隣り方向の橋脚との間に架けます。橋は斜めには架けられませんし、橋が交差することもできません。 The bridge is built between the piers in the up, down, left, and right directions. Bridges cannot be built diagonally, nor can bridges cross.
- 一方向には橋は二本までしか架けられません。 You can only have up to two bridges in one direction.
- 全ての橋脚は橋でつながっていなければなりません。 All piers must be connected by bridges.
橋をかけろの問題へ jump to Bridge problem.
解くコツ
Tips for solving
解くポイントは まずある橋脚の上下左右の隣方向の橋脚に掛けられる合計がちょうど指定本数になる所を探します。盤面の角にある④の橋脚、盤面の辺にある⑥の橋脚、盤面内にある⑧の橋脚ではかけられる橋を確定できます。
また盤面の角にある③の橋脚のように 二つの方向に最低1本の橋が架けられるところも注目です。 盤面の辺にある⑤の橋脚、盤面内にある⑦の橋脚でも各方向に最低1本の橋が架けられます。
各方向に架けることができる本数も変化してきます。ある橋脚の周囲に架けら橋の残りの数と その橋脚にあと架けなければいけない橋の残りの数が 一致している時は架けられるところすべてに掛けることになります。
特に最後の1本の橋を架ける方向が2か所ある時は橋の繋がりが切れないように架けることにも注意が必要です。 The point to solve is to find a place where the total number of piers that can be hung up, down, left, and right next to a certain pier is exactly the specified number.
On the pier ④ at the corner of the board, the pier ⑥ at the side of the board, the pier ⑧ at the inside of the board , two bridges can be built in each direction.
It is also worth noting that at least one bridge can be built in two directions, like the pier in ③ at the corner of the board.
At least one bridge can be built in each direction with the bridge pier ⑤ on the side of the board and the bridge pier ⑦ on inside the board.
The number that can be installed in each direction also changes.
If the number of bridges remaining around a pier and the remaining number of bridges that must be are the same, you will hang them all where you can.
Especially when the last one bridge has two directions, be careful not to break the connection of the bridge.
|
具体的に問題を解く手順を追って説明します。 次の図が問題です。 Here are the steps to solve the problem. The following figure is the problem. |
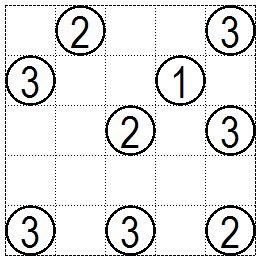
|
|
最上段の黄緑色の②は右方向にしか橋を架ける橋脚がありません。従って②から右の③には橋が2本架かります。 同じように2段目右にある水色の①の橋脚からは左の③にしか橋を架けられませんのでこの間に1本の橋が架かります。 The yellow-green ② at the top has a pier that can be bridged only to the right. Therefore, there are two bridges from ② to ③ on the right. In the same way, you can only build a bridge to the left ③ from the light blue pier ① at the right of the second step, so one bridge can be built between these piers. |
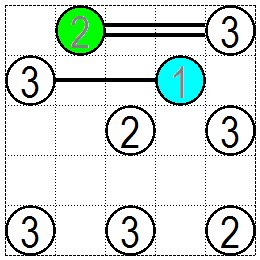
|
|
今度は左下の桃色の③を考えてみます。この橋脚からは上と右の2方向にしか橋を架けられません。
1方向には最大2本の橋しか架けられませんので少なくとも上と右に1本の橋は架かります。 (手筋の説明のため桃色の上の③から橋を架けていません。普通は上の③から2本の橋を架けるでしょう。) Now consider the pink ③ in the lower left. From this pier you can only build a bridge in two directions, up and right. At most two bridges can be built in one direction, at least on the up and right. (The bridge is not built from ③ on the pink color for explanation of ideas.Normally, two bridges will be built from above ③.) |
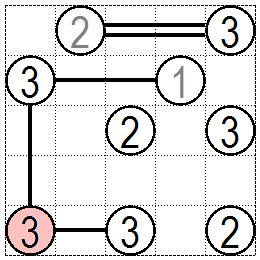
|
|
右上の水色の③からは既に左に2本橋が架かっており、残り1本ですが架けられる方向は下しかありませんので下に1本の橋が架かります。 また左上から2段目の黄緑色の③は右に1本、下に1本橋が架かっています。残り1本を架けなければいけませんが右側の橋脚①にはもう掛ける余裕がありません。 上方向にも橋脚がありませんので下方向にもう1本架け2本となります。 Two bridges have already been built to the left from the light blue ③ in the upper right, and there is only one remaining, but there is only one way to bridge, so one bridge is built below. In addition, yellow green ③ in the second row from the upper left has one bridge on the right and one bridge below.You have to build the remaining one, but there is no room for the pier ① on the right. There are no piers in the upper direction, so another one will be built in the lower direction. |
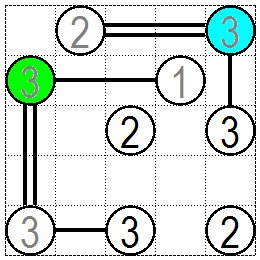
|
|
右端真ん中の黄色③にはあと2本の橋脚が架けられます。左方向にも下方向にも2本架けられる橋脚があります。 ここで下方向に2本の橋を架けたとしましょう。すると次図のように橋がすべて繋がらず 桃色の橋脚のグループと黄色の橋脚のグループ二つに分かれてしまいルール違反です。 同じように黄色の③から左方向の桃色の②に2本架けた時も橋が二つのグループに分かれてルール違反となります。 Two more piers are built on the yellow ③ in the middle of the right end. There are two piers that can be bridged both left and down. Now suppose you have built two bridges downward. Then, as shown in the next figure, all the bridges are not connected. It breaks into two groups: pink piers and yellow piers, which is a violation of the rules. Similarly, when two bridges are built from yellow ③ to pink ② on the left, the bridge is divided into two groups and it is a violation of the rules. |
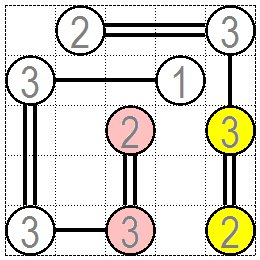
|
|
この結果黄色の③からは左の桃色の②に1本、下の黄色の②に1本の橋を架けるしかありません。 同じように最下段中央の桃色の③からは上の桃色の②へ1本、右の黄色の②へ1本架けることになり完成です。 As a result, there is no choice but to build one bridge from yellow ③ to pink ② on the left and one bridge to yellow ② below. Similarly, from the pink ③ in the center of the bottom row, one is attached to the upper pink ② and one to the right yellow ②. |
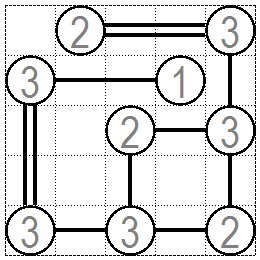
|
|
次に手筋のパターンを幾つか紹介しましょう。 次の図を見てください。水色の橋脚に注目してください。盤面角にある④、盤面辺にある⑥、盤面内にある⑧はそれぞれ橋が架けられる方向が 2方向、3方向、4方向ですので かけられる全ての方向に2本の橋が架けられます。 次は黄緑色です。盤面角にある③、盤面辺にある⑤、盤面内にある⑦は各方向に1本の橋がかかるか2本の橋がかかるかまだ分かっていませんが 少なくとも各方向に1本の橋は架けられます。 次は黄色に注目してください。黄色の②からは右に橋を架けても1本しかかけられませんので上に最低1本の橋が架けられます。 黄色の③では初期状態では右方向にも橋脚があり橋が架けられましたが 水色の⑧からの下方向の橋によりこの図では右方向には橋が架けられなくなっています。 このため盤面角の③と同じように二方向に1本ずつの橋が確定できます。 ある橋脚に橋を架けたことにより他の橋脚の橋が決められていきますので 架けた橋の周囲に注意しましょう。 ほかにもいろいろあります。橋が一つながりになるようにする場面も多々ありますので常にチェックしてください。 Next, let's introduce some solving patterns. See the following figure.Notice the light blue pier. There are two, three, and four directions in which the bridges can be built at ④ the corners of the board, at ⑥ the sides of the board, and at ⑧ the insides of the board, so two bridges can be built in all possible directions. Next is yellow-green cell. It is not yet known whether one or two bridges can be built in each direction at ③ on the corner of board, at ⑤ on the side of the board, or at ⑦ inside the board, but at least one bridge can be built in each direction. Next, notice the yellow cell.From the yellow ②, at least one bridge can be built on upward because only one bridge can be built on the right. In the initial state of yellow ③, there was a pier in the right direction, and the bridge was built. However, the bridge in the downward direction from light blue ⑧ makes it impossible to bridge in the right direction in this figure. For this reason, one bridge can be determined in each of the two directions in the same way as ③ of the board corner. When you build a bridge on one pier, the bridge on another pier will be decided. Pay attention to the area around the bridge. There are many others ways. There are many situations where the all bridges can be connected or not, so you would better to check always. |
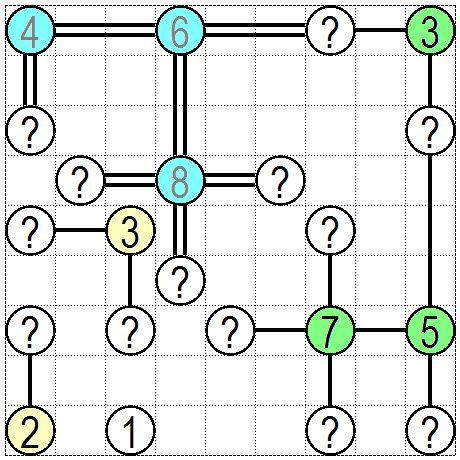
|
2020.2.28修正
2010.6.12作成
鴈野さんちのHomePage Top.
ご感想などは鴈野 敏生 まで。 2020.2.28 Modified
2010.6.12 First edition
Jump to top of Karino's HomePage.
mail to T.Karino