1. 矢印と数字の書かれた枡が問題枡で、数字はその位置から矢印の方向に入る黒枡の数を表しています。 The cell with the arrow and the number is the question cell, and the number represents the number of black cells that enter the direction of the arrow from that position.
2. 黒枡は縦横に並ぶことはありませんし、黒枡が盤面を分断することもありません。黒枡の隣枡は必ず問題枡か白枡です。 The black cell do not line up vertically and horizontally, and the black cell do not divide the board. The cell next to the black cell is always the problem cell or white cell.
3. 黒枡でも問題枡でもない枡（白枡）は必ず中心を通り辺と直行する線分が通過します。線分は枡の中心で曲がることはできますが分岐したり交差したり、途切れたりはできません。 Cell that are neither black nor problem cell (white cell) always pass through a line that passes through the center and goes straight to the side. Line segments can bend at the center of the cell but cannot branch, cross, or break.
4. 線分は最終的に一つの輪っかになります。輪が複数できたり途切れたりはしません。 The line segment eventually becomes a loop.There are not multi loops or breaks.
5. 問題数字での指定と関係のないところが黒枡になることもあります。 A place that has nothing to do with the specification in the problem may be a black cell.

ヤジリンの問題へ jump to YajiLin problem.

---

解くポイントはまず問題で指定された黒枡がぴたりと入るところが無いか探します。黒枡が決まればその周りは白枡になり必ず線分が通りますので マークをつけておくとよいでしょう。
ある枡の隣枡3か所が黒枡や盤面の端で行きどまりならその枡は黒枡になります。またある桝を黒枡にすると隣の枡が線分の袋小路になってしまう場合にはその枡は黒枡にできません。
線分を引ける方向が二つしかない白桝はその方向に線分が引かれます。
線分を引く時には小さなループが出来ないように引いて行くことも必要です。
それでは例題で説明します。
ここでの説明では黒枡になるか線分が通るか未定の枡は灰色で、線分が通っていたり　通ると決まった枡は白で表示しています。 印刷されたパズルを解く時には線分が通ると決まった枡には　中点（・）をつけておくのも良いでしょう。 The point to solve is to first find if there is any place where the black cell specified in the problem can enter. Once the black cell is determined, the area around it will be a white cell and the line will always pass. You may want to add a mark.
If three places next to a certain cell stop at a black cell or the edge of the board, the cell will be a black cell. In addition, if a certain cell becomes a black cell, if the next square becomes a dead-end of a line, that cell cannot be a black cell.
A white cell that has only two directions to draw a line is drawn in that direction.
When drawing a line segment, it is necessary to draw it so that a small loop cannot be formed.
Let me explain with an example.
In the explanation here, cells that are undetermined whether they will be black or pass through the line are gray, and cells that have passed or decided to pass a line are displayed in white. When solving printed puzzles, it is a good idea to add a midpoint (・) to the square that has been determined to pass the line cell.

次の図が問題です。矢印の付いた数字が書かれている枡が問題枡です。 The following figure is the problem. The cell with the number with the arrow is the problem cell.
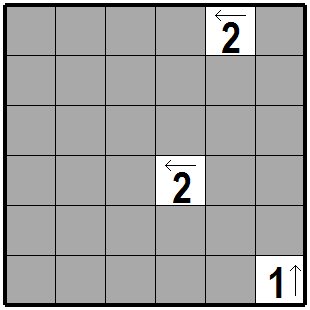
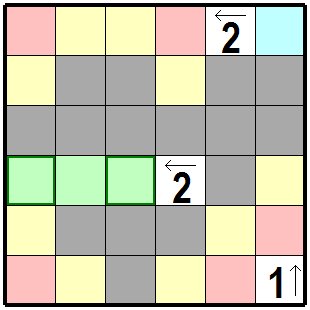
まずは中央付近の左矢印のついた２に注目してください。 これは　この枡の左側の三つの薄緑色の枡のうち二つが黒枡になるということです。 黒枡は二つ並ぶことはありませんので緑の枠のついた　両端の二つの枡が黒枡になります。ちょうど入りました。 右上隅の水色の枡は袋小路になりますので　黒枡になります。 また　黄色の枡に注目するとこの枡が黒枡になると隣のピンクの枡は白枡となり、途切れた線分しか引くことができない袋小路となりますので この黄色の枡は白枡でなければなりません。 First, notice the 2 with the left arrow near the center. This means that two of the three light green cells on the left side of this cell are black cells. There are no two black cascades, so the two green framed both end cells are black cell.Just entered. The light blue cell in the upper right corner is a dead end, so it is a black cell. Also, pay attention to the yellow cell, and when this cell becomes a black cell, the next pink cell becomes a white cell. And since it will be a dead end that can only draw broken lines. So this yellow cell must be a white cell.
ここまでで決まる白枡・黒枡が次の図ですが、ここでは決まった黒枡の周りの枡も白枡にしてあります。 ここで黒枡の周囲に注目すると白枡の周囲の辺４か所のうち２方向にしか線分が引けないものがいくつかあります。これらの枡の線分は その引ける方向に確定できます。 The white and black cell determined up to this point are shown in the following figure, here, the cell around the fixed black cell is also a white cell. Looking at the area around the black cell here, some of the four sides around the white cell can draw line segments in only two directions. The line segments of these cells. You can confirm in the direction that you can draw.
線分が確定できたものです。 ここで線分が引かれたことで中央近くの黒枡の上下の白枡についても線分が引けるのは２方向になりましたので線分が確定できます。 The line segment has been confirmed. Since the line segment was drawn here, the line segment can be drawn in two directions even for the white cells above and below the black cell near the center, so the line segment can be confirmed.
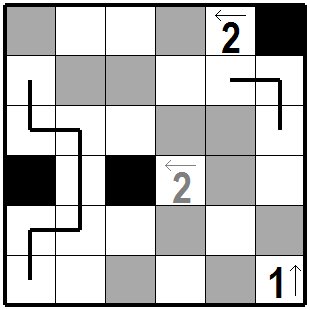
線分が確定できたものです。 ここで最上段の枡を考えてみます。左矢のついた２の左側には黒枡にできる枡が二つしか残っていませんのでこの二つは黒枡に決まります。 he line segment has been confirmed. Let's consider the top cell here. On the left side of 2 with the left arrow, there are only two space to be black left, so these two are determined as black cells.
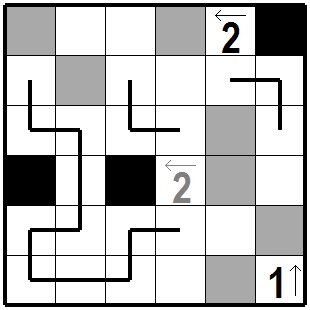
黒枡の周囲などでまた線分が確定できる枡があります。 右はじの縦列を考えてみますと、一番下に問題枡があり、この枡より上には黒枡が一つあるという指定になっていますが、 一番上の枡がすでに黒枡になっていますので残りの枡は白枡になります。 There is a cell where the line segment can be determined again around the black cell. Considering the column on the right, there is a problem cell at the bottom, and there is a black cell above this cell. But the top cell is already a black cell, so the remaining cells are white cells.
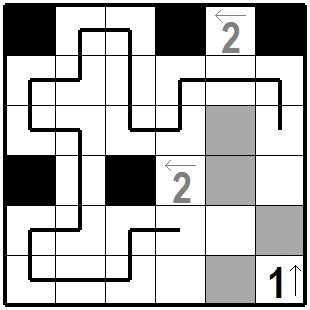
右端の縦列には既に黒枡1個ありますので一番下の問題枡1の上は白枡になりましたが、この問題枡１の左も白枡で無いとその左の白枡で線分が途切れて袋小路になってしまいます。 これでさらに線分が確定できるところが伸びます。 次の図まで来るとあと一息です。黒枡は二つ並ばないこと、線分は途切れずひとつの輪っかになることを考えると次の正解が得られます。 In the rightmost column, there is already one black square, so the top of the bottom problem square 1 is now a white cell. But if the left side of this problem cell 1 is not a white cell, the line segment will be cut off at the left white cell and it will become a dead end. This extends the place where the line segment can be determined. When you come to the next figure, you have a break. The following correct answer can be obtained considering that the two black mas are not lined up and that the line segments are one loop without interruption.
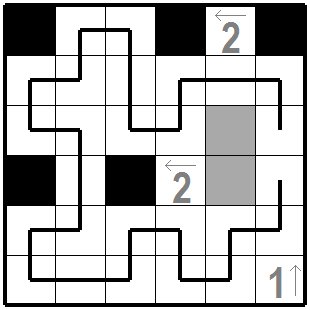
これが正解です。 This is the correct solution.
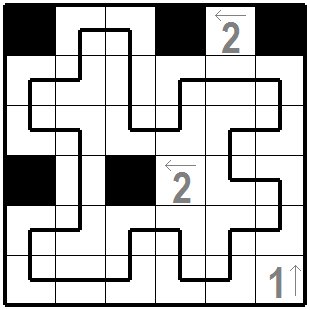
次にいくつかの黒枡・白桝・線分が決まるパターン（手筋）を紹介しておきます。なぜこうなるかを考えてみると良いでしょう。 次の図の左上緑色の0のように盤面端から縦横両方向二桝目が問題枡で盤面の端の枡（縦横斜め）が問題枡でなければ緑色の問題枡をぐるっと回るように線分が決まります。 また図で緑色枠で示した枡のように線分端から斜め位置にある枡で黒枡にすると線分が枝分かれしてしまう時には白桝になります。（図では他にもあります。　） 盤面の端を除いて黒枡がぴったり指定数入るのは　下左側の青色の2のように黒枡が一つおきに入る時ですが 盤面右側の青色3のように盤面の端にある時は他に黒枡や問題枡がなければ二つおきに黒枡が並びます。 また赤色の2のように　指定方向に同じ方向の黒枡数を指定されている時は　その差を考えると二つの問題枡の間で黒枡がぴったり指定数入ることもあります。 （赤い枠の黒枡） Next, I will introduce the pattern that determines some black cells, white cells, and line segments. It's a good idea to consider why this happens. If the second cell in both the vertical and horizontal directions from the edge of the board is a problem cell and the cell at the end of the board (vertical and horizontal diagonal) is not a problem cell, the line segment is determined so that it turns around the green cell as shown in the following figure. In addition, if a black cell is used as a cell that is obliquely located from the end of the line, as in the cell shown in the green frame in the figure, it will be a white cell when the line segment branches off. (There are others in the figure.) Except for the edge of the board, the black cell is exactly the specified number when it enters every other black cell, like the blue 2 on the lower left. But if there is no other black or problem cell at the edge of the table, such as blue 3 on the right side of the board, every third cell is black lined up. In addition, when the number of black cell in the same direction is specified in the specified direction, such as red 2, the number of black cell may be exactly the specified number between the two problem cells considering the difference.
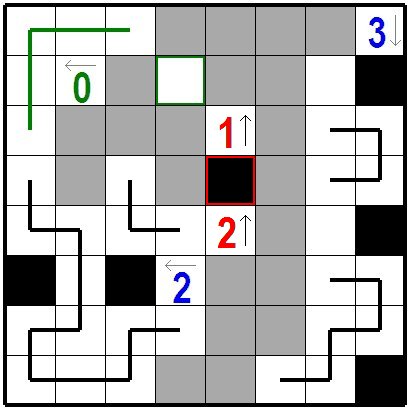
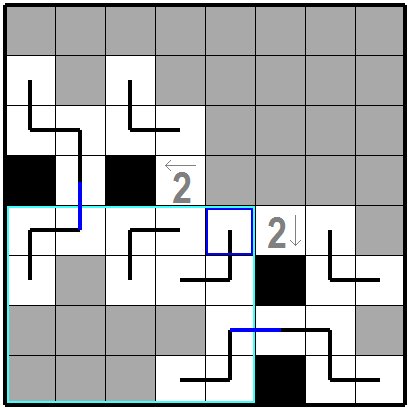
次の図を見てください。ここでは　二つの問題枡2で黒枡が決まり　それにより線分も何か所かひかれています。 ここで青色の枡に下から引かれた線分が次に上方向に引かれるか左方向に引かれるか考えてみます。 水色の領域にその外から引かれている線分を考えると青色の2本です。そこで青色枠の枡位置で上に引くと合計3本の線分が水色の領域から外部に引かれます。 奇数本引かれるとこの領域内で線分が途切れたり枝分かれすることになりルールに反します。従って青色枠の枡位置では線分が左に引かれます。 これ以外にもいろいろな手筋があります。 See the following figure. Here, the black cell is determined by the two problem cell 2 and the line segment is drawn several places. Here, let's consider whether the line drawn from below on the blue cell is drawn next upward or leftward. Considering the line segment drawn from the outside in the light blue area, it is two blue lines. So, if you draw upward at the position of the blue framed cell, a total of three line segments will be drawn outside from the light blue area. If an odd number is drawn, line segments will be interrupted or branched in this area, violating the rules. Therefore, a line segment is drawn to the left at the position of the blue frame. There are many other ways to do this.

---