1. 次の条件に合うよういくつかの枡を太線で囲まれた長方形のグループに分けていきます。 Divide some cells into rectangular groups surrounded by thick lines to meet the following conditions.
2. 白ぬきの数字が問題枡で、数字はこの枡を含む長方形のグループの枡の個数を示しています。 The white numbers in black circle are the problem cells, and the numbers indicate the number of cells in the rectangular group that includes this cell.
3. 太線で囲まれた長方形のグループには必ず一つの問題枡が入ります。入らなかったり、二つ入ってはいけません。 A rectangular group surrounded by a bold line always contains one problem cell. Do not enter the problem cell or do not enter two.
4. ある枡は一つのグループにのみ属し、二つ以上のグループに属することはありません。 A cell belongs to only one group and does not belong to more than one group.

四角に切れの問題へ jump to Shikaku problem.

---

まず問題で与えられた数となる長方形の種類を考えてみます。③であれば1×3と3×1の長方形しかありませんが、 ⑫であれば1×12、12×1、2×6、6×2、3×4、4×3と6通りあります。
始めは大きな数字や、組み合わせ数の少ない3,5,7などの数字に注目します。
これらの数字で一通りしか四角形を決めようがない所からまず四角形を決めましょう。
それでは例題で説明します。
First consider the type of rectangle given in the problem number. In case of ③, there are only 1 × 3 and 3 × 1 rectangles, For ⑫, there are six types, 1 × 12, 12 × 1, 2 × 6, 6 × 2, 3 × 4, 4 × 3.
At first focus on large numbers or numbers with few combinations such as 3,5,7.
First of all, let's decide the rectangle from the place where it is impossible to decide the rectangle except one combination by these numbers.
Let me explain with an example.

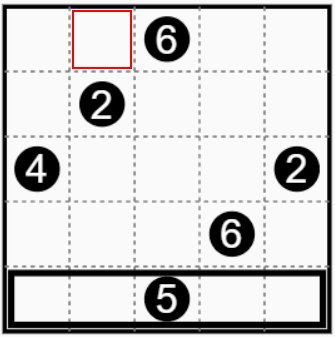
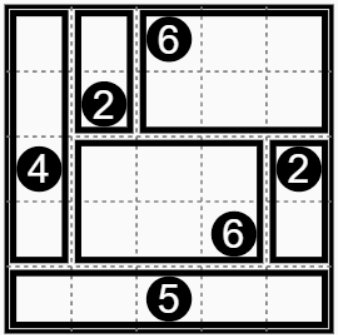
次の図が問題です。数字の入った枡が問題枡です。 ここでは最下行の⑤に注目してください。枡の数が５となる長方形は1×5と5×1しかありません。 この問題枡を含めて縦に5個並んだグループか、横に5個並んだグループを作るのですが、 一番上の行に⑥があるため縦に5個並んだグループは作れません。 The following figure is the problem. Cells with numbers are the problem. Here, please pay attention to ⑤ on the bottom line.There are only 1 × 5 and 5 × 1 rectangles that have 5 cells. We will make a group of 5 vertically or a group of 5 horizontally including this problem square, Because there is a ⑥ in the top row, you cannot make a group of 5 vertically.
次の図のように最下行は横1列のグループとなります。 次は一番上の行の⑥を見てみます。枡の数が６となる長方形は1×6、6×1、2×3、3×2の４通りありますが、この問題では6個並んだ枡のグループは作れませんので 2×3、3×2の長方形となります。今のところこの最上段の⑥を含む長方形は2×3、3×2どちらも作れますが、左となりの赤い枠の枡はこれらの長方形には属しません。 するとこの赤い枠の枡を含む長方形はその下の②の枡と組み合わせて1×2の長方形を作るしかありません。 As shown in the following figure, the bottom row is a group of one horizontal row with five cells. Next, let's look at ⑥ in the top line. There are four types of rectangles with the number of cell of 6: 1 × 6, 6 × 1, 2 × 3, 3 × 2. In this problem, it is not possible to create a group of 6 cells. It becomes a 2x3, 3x2 rectangle. Right now, you can make both 2x3 and 3x2 rectangles that include the top ⑥, but the red framed cell on the left does not belong to these rectangles. Then, the rectangle containing this red frame can only be combined with the cell ② below to create a 1x2 rectangle.
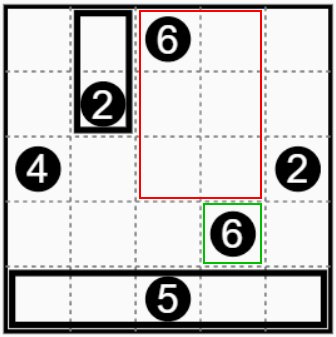
もう一度最上段の⑥で考えてみます。 この⑥を含むグループは2×3か3×2とできます。2×3のグループは次のように赤い枠の枡で構成できますが このようなグループを作ると下から２段目にある緑色の枠の問題枡⑥で指定された6個の枡のグループを作ることができなくなってしまいます。 従って最上段の問題枡⑥で指定されたグループは3×2のグループとなります。 この問題では3×2のグループの作り方は一通りしかありませんでしたが複数の作り方があるのが普通ですので見落とさないよう注意が必要です。 Let's think again at the top ⑥. The group containing this ⑥ can be 2 × 3 or 3 × 2. A 2x3 group can be composed of a red frame as shown below but if you create such a group, you will not be able to create a group of six cells specified by the green problem cell ⑥ in the second row from the bottom. Therefore, the group specified by the problem cell ⑥ at the top is a 3 × 2 group. In this problem, there was only one way to create a 3x2 group, but there are usually multiple ways to create a group, so be careful not to overlook it.
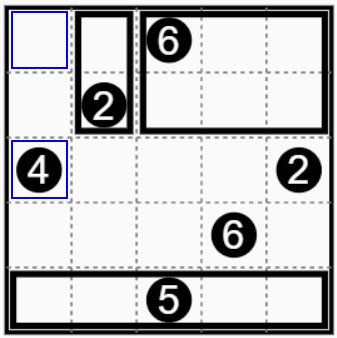
今度は左上の青い枠の枡を考えてみます。この枡を含むグループはこの枠の二つ下の問題枡④で指定された４個の枡のグループしか作れません。 Now consider the blue framed cell in the upper left corner. A group that includes this cell can only create a group of four cells specified by the problem cell ④ 2 below this cell.
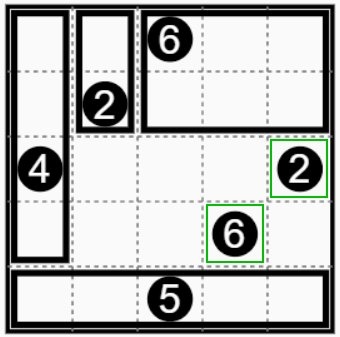
あとは緑色の枠の②と⑥で指定された二つの長方形に分けるだけです。 All you have to do is divide it into two rectangles designated by the green frame ② and ⑥.
これが正解です。 This is the correct solution.

---