1. 次の条件に合うよう各枡に数字を入れていきます。 Enter numbers in each cell to meet the following conditions.
2. 太い枠線で囲われた1個以上の連続した枡は同一グループで、同一グループの中には１からグループの枡数までの数字がはいりますが、同じ数字は同じグループには入りません。 One or more continuous cells surrounded by a thick frame are in the same group, and the same group contains numbers from 1 to the number of cells in the group, but the same number does not belong to the same group.
3. あらかじめ数字が問題数字として配置されている場合もあります。枡に入る数字の左右上下方向の枡に同じ数字がある場合はその数字と同じ数以上の間隔が無ければいけません。 （２数字の間には他の数字の枡が入っている）例えば3が同じ列の他の枡に入っている時には３の入っている枡と枡の間に３個以上他の数字の入った枡が無いといけません。 The numbers may be arranged as problem numbers in advance. If there is the same number in the left, right, up, and down direction of the number to enter the cell, there must be an interval of the same number or more. For example, when 3 is in another cell in the same row, there must be at least 3 cells with other numbers between the cells containing 3 cells.

波及効果の問題へ jump to RippleEffect problem.

---

解くポイントはまず太線で囲まれたいくつかの枡からなるグループの中で数字の決まっていない枡が一つなら残り一つの数字が決まります。
またあるグループの中にある数字の決まっていない枡では　そこにはこのグループの枡数までの数字しか入りませんが上下左右に間隔が十分ある数字が一つしかないならその数字に決まります。
さらにグループで既に決まっていない数字・上下左右に間隔が十分ある数字が一つならその数字に決まります。
数字が未定の枡に　入る可能性のある候補数字をメモ書きし、周囲の数字が決まった時に候補メモを修正していくのも良いでしょう。 The point to be solved is that if there is one unnumbered cell in a group consisting of several cells enclosed by a thick line, the remaining number will be determined.
Also, if a cell in a group has an undetermined number, it will only contain numbers up to the number of cells in this group, but if there is only one number that has sufficient space above, below, left, and right, that number will be determined.
It is a good idea to write down the candidate numbers that may enter the unspecified cell, and then modify the candidate notes when the surrounding numbers are determined.

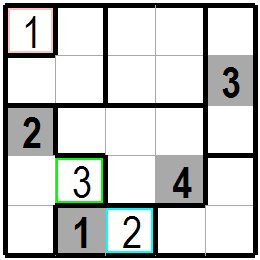
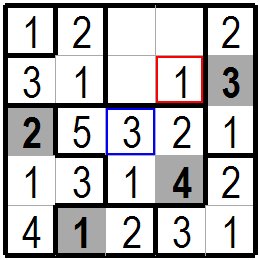
実際の問題で説明します。次の図が問題です。 網の掛かった太い数字の枡が問題枡です。（ここでは問題数字がはっきりするよう網をかけていますが問題数字が太字の時もあります。） Let's explain with a real problem. The following figure is the problem. The problem cell is a large numbered cell with a net. (The problem numbers are shaded here to make them clear, but sometimes they are bold.)
まずは同じグループで数字が決まっていない枡が一つのところに注目します。 1行目の左端の桃色の枠の枡は枡一つのグループですので１が入ります。 また 一番下の水色の枠の枡は二つの枡のグループで、左隣の枡には既に１が入っていますので２が入ります。 次は4行目の黄緑色の枠の枡を考えます。この枡はトの字型の四つの枡のグループですので1～4の数字が入りますが、同じグループに既に2が入っており、下隣（間隔0）に1が入っていますので２と１は入りません。 さらに右側二つ目には４があるため４枡空けないと４は入れられません。結局入れられる数字は３になります First, notice that there is only one square in the same group whose number is not determined. The pink framed cell on the left end of the first row is a group of one cell, so 1 is entered. The cell with the light blue frame at the bottom is a group of two cells. The cell on the left is already filled with 1, so 2 will be entered. Next, consider the cell with a yellow-green frame on the fourth line. Since this square is a group of four squares , the numbers 1 to 4 will be included, but 2 is already in the same group and 1 is in the lower area (interval 0) so 1 and 2 do'nt enter. Furthermore, there is 4 in the second on the right side, so 4 can not be entered unless 4 spaces are left. After all, the number entered is 3.
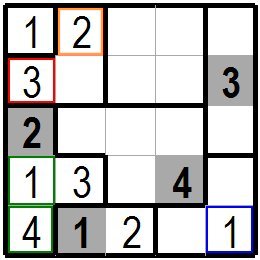
左上端の１が入った周りの逆L型の三つの枡のグループを考えて見ます。前の図で上から4枡目、左から２枡目の黄緑色の枠に３が入りましたのでこの枡から上の３枡には３が入れません。 従って逆L型の３枡のグループでは上から２枡目の左端の赤色の枠の枡にしか３がはいれないことになります。 この枡の上に1があり　下に２があるため3しか入れられないとも考えられます。 逆Lのグループの残りの二枡には１と２が入りますが、 最上端の左から２枡目の橙色の枠の枡は左隣に１が入っていますので１は入れられず残りの２が入ります。 次は左端の上から3～5枡目にある（緑色枠の1枡を含む）トの字型の4枡のグループを考えてみます。この4つの枡のグループには1～4が入りますがすでに２と３は入っています。 また上から4桝目、左から4枡目（緑色枠1の右3枡目）に４があるのでその左４枡（実際は３枡ですが）には４が入れず、 ４は上から５枡目、左端の緑色の枠の枡にしか入れません。残りの１は空いている上から4桝目、左端のの緑色の枠の枡に入ります。 今度は右下隅の青色枠の枡を含む逆L型の３枡のグループを考えます。このグループには1～3が入ります。このグループの上から５枡目、左から５枡目の右下隅の青色の枠の枡を考えます。 この枡の左２枡目には2があり、上３枡目には３がありますのでこの枡には２も３も入れませんので残りの１が入ります。（1の上の枡に2、左の枡に3が決まるので残りの1が青色枠の枡に入るとも考えられます。） Let's consider a group of three inverted L-shaped cells with the upper left 1. In the previous figure, 3 was placed in the yellow-green frame of the fourth cell from the top and the second cell from the left, so 3 could not be entered in the three cells above this cell. Therefore, in a group of three inverted L-shaped cells, only 3 can be inserted into the red framed cell at the left end and second raw from the top. It is thought that only 3 can be inserted because there is 1 above this cell and 2 below it. The remaining two cells of the group of inverse L will be filled with 1 and 2,but in the orange frame of the second cell from the left at the top, 1 is on the left, so 1 cannot be entered and the remaining 2 will be entered. Next, let's consider a group of four cells that are 3rd to 5th cells from the top left (including one cellwith a green frame). This group of four cells contains 1-4, but already has 2 and 3. There are 4 in the 4th cell from the top and the 4th cell from the left (the 3rd cell on the right of the green frame 1), so 4 is not inserted in the 4 cells on the left (actually 3 cells). So 4 can only be placed in the 5th cell from the top, the cell with the green frame at the left end. The remaining 1 goes into the fourth cell from the top and left end,which is vacant and green framed. Now consider a group of three inverted L-shaped cells, including a cell with a blue frame in the lower right corner. This group contains 1-3. Consider a cell of this group which is a blue framed cell of the fifth cell from the top and the fifth cell from the left at the lower right corner. There are 2 in the 2nd cell on the left and 3 in the 3rd cell on the top, so neither 2 nor 3 can be put in this cell, so the remaining 1 will be inserted. (Since 2 is determined for the cell on the top and 3 for the cell on the left, it is considered that the remaining 1 enters the cell with the blue frame.)
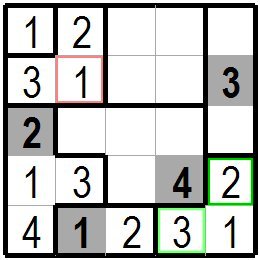
先ほどの右下隅の逆L型の三つの枡のグループをもう一度考えます。上から5枡目、左から4枡目の黄緑色の枠の1の左の枡は隣に２がありますので２が入れず残った３が入ります。 右から5桝目、上から4枡目の1の上の緑色の枠の残った枡は残りの数２が入ります。 また左上の逆L型の3枡のグループの空いていた上から２枡目、左から２枡目の桃色の枠の枡には残った数字１が入ります。 Consider again the group of three inverted L-shaped cells in the lower right corner. There is 2 next to the cell on the left of 1 in the yellow-green frame of the 5th cell from the top and the 4th cell from the left, so the remaining 3 will be entered without entering 2. The remaining cells with a green frame above the cell 1 in the fifth cell from the right and the fourth cell from the top contain the remaining number 2. The remaining number 1 is entered in the pink frame of the second cell from the top and the second cell from the left of the group of three inverted L-shaped cells in the upper left.
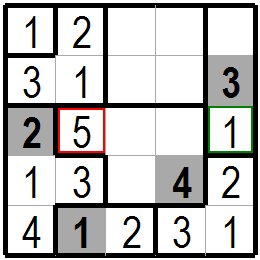
こんどは上から３～４桝目、左から２～４桝目にある赤色枠の枡を含む五つの枡のグループを考えます。この五つの枡には1～5 の数字が入りますが、4は既に同じグループの上から４桝目左から４桝目に入っています。 上から３桝目、左から２枡目の赤色の枠の枡を考えて見るとこの枡の上には１が、左には2が、下には3がありますので１～３は入りません。４は既に同じグループの他の枡で使われていますので、この枡には５しか入れられません。 次に右端の上から１～３枡目にあるI型の3枡のグループを考えます。上から2枡目には既に3が入っています。上から３枡目の緑色の枠の枡を考えると直ぐ下隣の枡に２が入っていますので２も入れず、残りの１が入ります。 上から５枡目の最下端の枡に１が入っていますが間のひと枡に違う数字２が入っていますので上から３桝目に１は入れます。 This time, we will consider a group of five red framed cells which are 3rd to 4th squares from the top and 2nd to 4th cells from the left. These five cells are filled with numbers from 1 to 5, but 4 is already in the fourth cell from the top and left of the same group. If you look at the red cell of the third cell from the top and the second cell from the left, there are 1 on the upper cell, 2 on the left, and 3 on the bottom, so 1-3 are not included. Since 4 is already used by another cell in the same group, only 5 can be placed in this cell. Next, consider a group of three I-shaped cells located in the first to third squares from the top right. 3 is already in the second cell from the top. Considering the green cell of the third cell from the top, the cell next to it contains 2 immediately, so 2 is not included and the remaining 1 is included. There is a 1 in the bottom cell of the fifth cell from the top, but a different number 2 in one cell between them, so put a 1 in the third cell from the top.
ここまで来ればあとは図を見ていただければ分かるでしょう。 If you come to this point, you can see the figure afterwards.
これが正解です。 This is the correct solution.
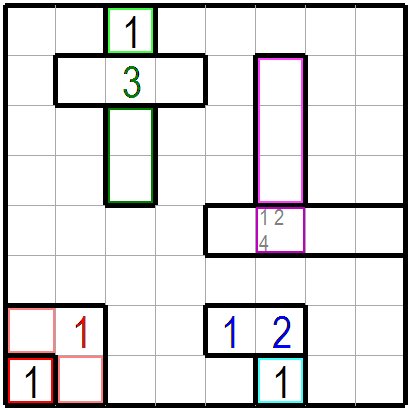
つぎはいくつか手筋を紹介します。 次の図の下中央部の水色枠の一枡には1が入りますので上に接した二枡には青数字のように2,1が入ります。 図の左下の赤色枠の一枡には1が入りますので隣の桃色の二つの枡には1を入れられません。すると残り一桝に1（赤字）を入れるしかありません。 図の上部の一枡と二枡に挟まれた三枡のグループを考えてみます。黄緑色枠の一枡には1が入り、 緑色枠の二桝のどちらに2が入っても三枡の中央の枡には1も2も入れられず3が入ります。 図の右側にある薄紫枠の三枡ではどこかに3が入ります。このため三枡グループに接した紫色枠の枡には3が入れられず、1,2,4が候補数字として残ります。 The following are some tips. In the figure below, one cell in the light blue frame at the bottom center contains 1, so the two cells in contact with the top contain 2,1 as blue numbers. 1 is entered in one cell of the red frame at the lower left of the figure, so 1 cannot be entered in the two adjacent pink cells. Then there is no choice but to put (red) 1 in the remaining cell. Consider a group of three cells sandwiched between one cell group and two cell group at the top of the figure. One cell in the yellow-green frame is filled with 1, and no matter which of the two cells in the green frame is filled with 2, neither the cell 1 nor the cell 2 can't be filled in the center of the three cells, so this cell can be filled with 3. In the light purple frame on the right side of the figure, there is a 3 somewhere. For this reason, 3 is not put in the purple frame of the cell in contact with the three cell groups, and 1, 2, and 4 remain as candidate numbers of this cell.
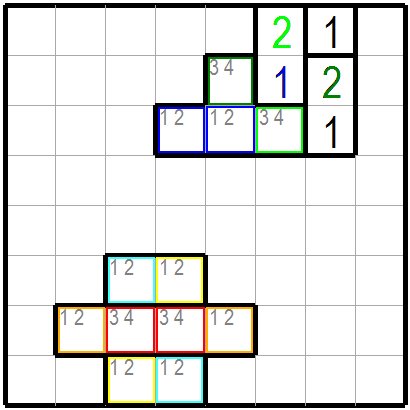
次の図の上部の一枡と二枡接したところでは　図のように緑色/黄緑色の2、青色の1などのように決まります。その左の山形の4枡のグループで考えます。 緑色枠の枡では右側に青色の1、緑色の2があり1と2は入りませんので候補として3,4が残ります。 黄緑色枠の枡では上側に青色の1、黄緑色の2があり1と2は入りませんので候補として3,4が残ります。 山形の四枡のうち二枡で3と4が候補としてあるため残りの枡には3,4を入れられません。従って青色枠の二つの枡には1,2が候補数字として残ります。 下部の二枡と四枡が接したところでは　二つの水色枠が2、二つの黄色枠が1になるか、二つの水色枠が1、二つの黄色枠が2になるかしかありません。 すると、水色枠と黄色枠に挟まれた二つの赤色枠の枡には1と2は入れられませんので候補数字として3,4が残ります。 橙色枠の枡には2か所で予約された3,4は入れられませんので　橙色枠の枡2か所には1,2が候補数字として残ります。 他にもいろいろのパターンがあります。 In the following figure, where two cells group are in contact with the one cell group, they are determined as green / yellow green 2, blue 1, etc. Think in a group of four cell on the left of them. In the green frame, there are blue 1 and green 2 on the right side, and 1 and 2 are not included, so 3, 4 remains as candidates. In the yellow-green framed cell, there are blue 1 and yellow-green 2 on the upper side, and 1 and 2 do not enter, so 3, 4 will remain as candidates. In the four cell group, candidates of two cells are 3 and 4, so 3 and 4 cannot be entered in the remaining cell. Therefore, 1 and 2 remain as candidate numbers in the two cells in the blue frame. Where the lower two cells group meet the four cells group, there are only two light blue frames at 2, two yellow frames at 1, or two light blue frames at 1, and two yellow frames at 2. Then, 1 and 2 can not be entered in the two red frame cells sandwiched between the light blue frame and the yellow frame, so 3, 4 will remain as candidate numbers of them. 3 and 4 reserved in two places cannot be entered in the orange frame, so 1,2 will remain as candidate numbers in the two orange frames. There are many other patterns.

---