1. 太線で囲まれた桝のグループに二つ黒枡を置きます。 残りの枡は白枡です。 Put two black cells on a group of cell enclosed by thick lines. The remaining cell is a white cell.
2. 盤面上の黒枡は全て縦または横に二つ並びます。一つだけだったり、三つ以上の塊ができてはいけません。 All the black cells on the board are arranged vertically or horizontally. There must not be only one or more than two clumps.

---

解くポイントはまず二枡のグループを探します。ここはどちらの枡も黒枡に決まります。二桝並んだ黒枡が決まったらその上下左右の枡は黒枡には出来ませんので白桝のマークをしておくと良いでしょう。
まだ黒枡が一つもないグループでも白黒決まっていない枡が二つしか残っていなければその二桝は黒枡になりますし、 白黒決まってない枡が残り一つでそのグループに入れる黒枡の残りが一つなら残り一つの枡も黒枡になります。
白黒決まっていない一桝の上下左右の隣枡が白桝になるならその枡は白桝になります。
黒枡が決まったあとその上下左右で黒枡にできる枡が一つならそこを黒枡にして二桝の黒枡の塊にします。
近くに黒枡に決まっている一つの枡が二か所以上ある時は　それぞれの枡が黒枡2枡になった時繋がって3枡以上の黒枡の塊にならないように注意します。
それでは例題で説明します。
以下の説明では白黒決定の手順がはっきりするよう未定の枡は灰色で表示しています。実際のパズルでは黒枡以外はすべて白枡として扱っています。 The point to solve is to first find a group of two cells. Here, both cell is determined to be a black cell. Once the two black cells are lined up, the upper, lower, left and right cells cannot be black, so it is better to mark them as white cells.
If there are only two cells which are not decided black or white left in a group with no black cell yet, the two cells will be black cells. and if there are only one cell which are not decided black or white left in a group with one black cell yet, the remained cell will be black cell.
If the top, bottom, left and right neighbors of an undetermined black cell and white cell are white cells, the center cell is a white cell.
After the black cell is decided, if there is one cell that can be made into black cell at the top, bottom, left and right neighbors, it is made into a black cell and it is made into two block of black cell.
When there is more than one place that is determined to be a black cell nearby, and when each cell becomes two black cell, be careful not to connect them to form a mass of three or more black cell.

Let me explain with an example. In the following explanation, undetermined cells are shown in gray to make the procedure for determining black and white clear. In the actual puzzle, everything except black cell is treated as white cell.

次の図が問題です。太い線がグループの境界線です。 まずは二枡のグループを探しその二枡を黒枡にします。 The following figure is the problem.The thick line is the group border. First, find a group of two cells, and make them two black cells.
二枡連続の黒枡の塊ができたら上下左右の隣枡は白枡です。 ここで左下の三枡のグループを見ると内一枡は白枡になっていますので残りの青色枠の二枡は黒枡になります。 また黄緑色枠の枡は上下左右が白桝ですのでこの枡を黒枡にしても二枡の黒枡の塊にできませんので白枡になります。 When two cells of black are formed in a row, the top, bottom, left and right neighbors are white. If you look at the group of three cells at the bottom left, one of the cells is a white, so the remaining two cellss in the blue frame are black. In addition, since the top, bottom, left, and right of the square with a yellow-green frame are white, even if this cell is a black cell, it cannot be made into a block of two black cell, so it will be a white cell.
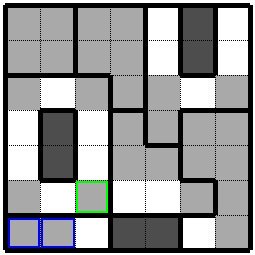
次は左側のロの字形のグループを考えてみます。このグループでは白黒決まっていない枡が黄緑枠の二枡で、 黒枡は一つもありませんのでこの黄緑色枠の枡は黒枡になります。 Next, let's consider the group of cells on the left. In this group, the cells which are undecided to black or white are two with yellow-green framed, and there is no black cell, so the yellow-green framed cells are black cells.
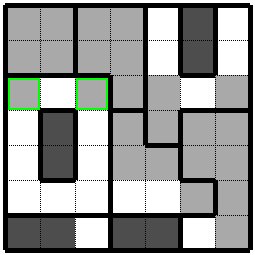
次は左の水色枠の黒枡はその上の水色枠の方にしか拡張できませんので水色枠の枡はどちらも黒枡になります。 一方青色枠の黒枡はその上と右に拡張できますのでここではどちらを黒枡にするか決められませんので保留しておきます。 Next, the black cell in the light blue frame on the left can be extended only to the light blue frame above them, so both the cells in the light blue frame will be black cell. On the other hand, since the black cell in the blue frame can be extended to the top and right, it is not possible to decide which one is the black cell here, so reserve it.
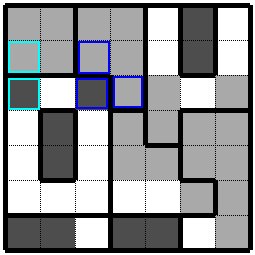
左上の四枡のグループでは黄緑色枠の枡がグループ二つ目の黒枡になり、その右にしか拡張できませんので右側の黄緑色枠の枡も黒枡になります。 In the group of four cells on the upper left, the yellow-green frame is the second black cell in the group. Since it can be expanded only to the right, the cell in the yellow-green frame on the right side also becomes a black cell.
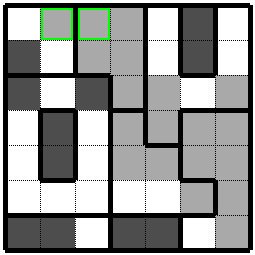
次は先ほど保留しておいた青色枠の枡は右側にしか拡張できなくなりましたので右側の青色枠の枡は黒枡になります。 Next, the cell with the blue frame that was reserved earlier can only be expanded to the right, so the cell with the blue frame on the right becomes a black cell.
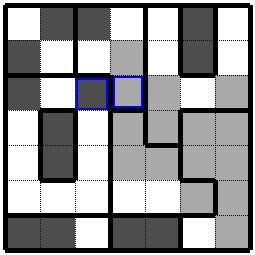
右上のグループでは白黒決まっていなかった水色枠と黄緑色枠の二つの枡が黒枡となり、 水色枠の下の枡が黒枡に決まりますので黄緑色枠の枡の下の枡も黒枡に決まります。 In the upper right group, the two cells, the light blue frame and the yellow-green frame, which were not determined in black and white, became black cells, The cell under the light blue frame is determined as the black cell, so the cell under the yellow-green cell is also determined as the black cell.
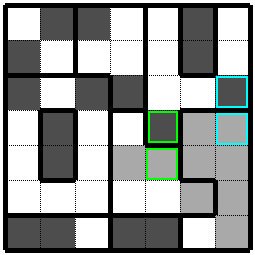
最後は青色枠の枡二つが黒枡となります。 At the end, the two cells with the blue frame are the black cells.
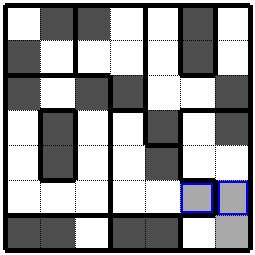
これが正解です。 This is the correct solution.
次に手筋のパターンを幾つか紹介しましょう。図は説明のためなので解ける問題にはなっていません。 次の図を見てください。二枡に隣接したところではすぐに黒枡が決まることがあります。 二枡に隣接した三枡のグループを見てみます。右上では紫色の枡は黒枡になります。その下のL字型の三枡では水色のように決まります。 次は四枡では左のように青色枡が黒枡に決まります。またL字形の四枡では水色枠の黒枡から赤色枠の枡に黒枡を拡張するともう一つの黒枡を入れる場所がありませんので黄色枠の枡二つが黒枡になります。 また左の六枡のように両側を二枡の黒枡に挟まれていると中央の黄緑色枠の枡が黒枡になります。 解くのになれるまでは白桝のマークをしっかりつけておくと黒枡位置を見つけやすくなります。 Next, let's introduce some patterns of solving method.The diagram is for illustrative purposes and is not a solvable problem. See the following figure. A black cell may be determined immediately next to a group of two cells. Let's look at a group of three cells adjacent to two cells group. In the upper right, the purple cell becomes a blackcell.The L-shaped three cells under it, it is determined like light blue. Next, in the four cells, the blue cell is determined as the black cell as shown on the left. Also, in the L-shaped four cells, if the black cell is expanded from the light blue cell to the red cell, there is no place for another black cell, so two cells in the yellow cell become black cells. In addition, when the two sides are sandwiched between two black ones like the six left ones, the yellow-green frame in the center becomes the black one. Until you can solve it smoothly, it is easier to find the position of the black cell if you mark the white cell firmly.
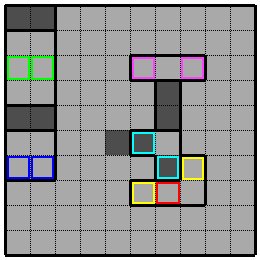
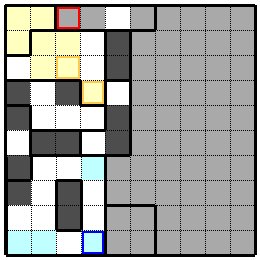
次の図の左下の水色の枡のあるグループで考えてみます。このグループには現在一つの黒枡があります。もう一つ黒枡を決めねばなりませんが水色の枡の一つを黒枡にすると他のグループにある隣枡も黒枡にする必要があります。他のグループに拡張できる枡は青色枠の枡だけですので青色枠の枡が黒枡になります。 こんどは左上のクリーム色の二つのグループで考えます。オレンジ色枠のどちらかが黒枡になりますので　今のところクリーム色のグループに奇数の黒枡があります。各グループに二枡ずつ黒枡を入れるためには偶数個にしなければなりません。すると一桝はこれらのグループ以外の枡とペアにしなければなりませんが、他のグループの枡でペアになれる枡は赤枠の枡しかありませんので赤枠の枡は黒枡になります。 このほかにも手筋はいろいろあります。自分で考え見つけた手筋を覚えておくと早く解くことができます。 Consider the group with a light blue cell in the lower left of the following figure.This group currently has one black cell. You have to decide on another black cell, but if one of the light blue cell is a black cell, the next cell in the other group must also be a black cell. The only cell that can be expanded to other groups is the cell with the blue frame, so the cell with the blue frame becomes the black cell. Let's think of two cream colored groups in the upper left. Either of the orange frames will be a black cell, so at the moment there are an odd number of black cells in the cream group. In order to add two black mas to each group, the number of black cells must be even. Then one cell must be paired with a cell other than these groups The only other cells that can be paired with other group cells is red framed cell, so red framed cell is black cell. There are many other methods.You can solve it faster if you remember what you think and find.

---