1. 次の条件に合うように各枡を白枡か黒枡に設定します。 Set each cell as a white cell or a black cell to meet the following conditions.
2. 問題で指定された数字はこの枡から縦横に連続した白枡の数を指定します。白枡の連続は枠の端点か黒枡で終了します。 The number specified in the problem specifies the number of white cells that are continuous vertically and horizontally from this cell. The continuation of the white cell ends at the end of the frame or at the black cell.
3. 黒枡の上下左右の隣枡は白枡になります。 The next, upper, lower, left, and right sides of the black cell are white cells.
4. 斜めに繋がった黒枡が盤面を分断することはありません。（すべての白枡は上下左右の白枡で一つながりになります。） Diagonally connected black cells do not separate the board. (All white cells are connected by top, bottom, left and right white cells.)

---

解くポイントは、ある枡が黒になるとその上下左右の枡は白枡になるわけですが、この結果問題数字で指定された数を超えてしまうとすると最初の黒枡指定がおかしかったことになりますのでこの枡は白枡です。この例として②と指定された問題枡の肩の位置（たとえば右上）の枡は白枡になります。
またある枡を白枡にしないと問題で指定された白枡数にならない枡は白枡になります。この例として９×９枡の問題で左上隅に⑪という問題数字指定されていれば、左端の列の上から三つの枡と上端行の左から三つの枡は白枡になります。
このようなところから注目していきます。

それでは例題で説明します。 The point to be solved is that when a certain cell becomes black, the upper, lower, left and right cells become white cells, but if the number of white cells exceeds the number specified by the problem number, the first black cell specification was incorrect. So this is a white cell. In this example, the cell at the shoulder position (for example, upper right) of the problem cell specified as ② is a white cell.
Also, if you do not make a certain cell a white cell, the cell that does not reach the number of white cells specified in the question will be a white cell.As an example, if the problem number is designated as “⑪” in the upper left corner in a 9 × 9 cells problem, the three cells from the top of the left column and the three cells from the left of the top row are white cells.
Let's pay attention from such a place.
Let me explain with an example.

次の図が問題です。左上の②の問題枡に注目します。 The following figure is the problem. Pay attention to the problem cell ② in the upper left.
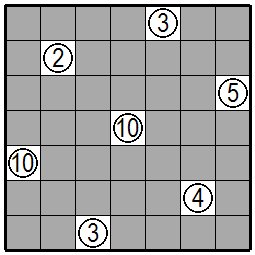
まず黄色の枠の枡に注目してください。 この黄色の枠の枡のどれでも黒枡にすると②の枡の上下左右の枡の２箇所が白枡になり、②の枡からの白枡の連続が３となり指定の２を越えてしまいます。したがって黄色の枠の枡４箇所は白枡になります。 また緑の枠の枡のどちらかが白枡になると②の枡からの白枡の連続は指定の２になりますので白枡連続の端点は黒枡になります。どちらの緑の枠の枡が白枡になっても赤の枠の枡２箇所が黒枡になりますが、そうすると左上端の白枡が黒枡で分割されてしまいます。これは最初の緑の枠の枡を白枡にしたのが間違いですので緑の枠の枡２箇所は黒枡でなければなりません。 黒枡の上下左右の枡は白枡になります。 First, pay attention to the yellow frame cell. If any of these yellow frames are black, two cells of the upper, lower, left, and right sides of the cell ② will become white, and the number of white cells from the cell ② will be three, exceeding the specified two.Therefore, the four squares in the yellow frame are white. In addition, if either of the green cells is a white cell, the continuation of the white cell from the cell ② will be the specified 2, so the end point of the white cell is a black cell. Whichever green frame is white, two red frames are black, but the upper left corner is split by black. It is wrong to change the first green frame to a white one, so the two green frames must be black. The top, bottom, left, and right of the black cell are white cell.
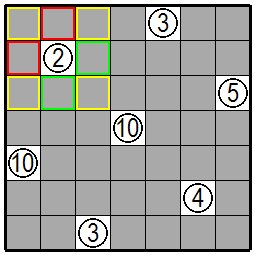
今度は左端の⑩の問題枡に注目します。左端の列が上から下まですべて白枡になっても白枡の連続は７にしかなりませんので⑩の右側３枡（黄色の枠の枡）は白枡になります。 また⑩のある上から５行目の枡がすべて白枡になっても白枡の連続は７、さらに⑩の下の枡もすべて白枡にしても白枡の連続は９にしかなりませんので⑩の上の枡ひとつ（緑色の枠の枡）も白枡になります。 This time, pay attention to the problem cell ⑩ at the left end. Even if the leftmost column is all white from the top to the bottom, the continuity of the white cells is only 7 so the three cells on the right side of ⑩(yellow frame) are white cells. Also, even if all of the cells in the fifth row from the top with ⑩ become white, the continuity of white cells will be 7 even if the cells under ⑩ are all white. One cell above the cell ⑩ (green frame cell) is also a white cell.
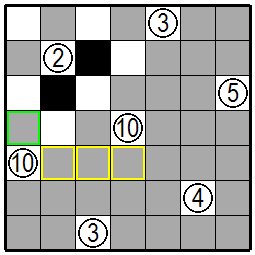
今度は最下段の③に注目します。③の肩の位置の緑色の枠の枡のひとつが黒枡になったとすると黄色の枠の枡と赤色の枠の枡のひとつが白枡となり、白枡の連続が４となり問題で指定の３を超えてしまいます。したがってこの緑色の枠の枡２箇所は白枡でないといけません。 This time, focus on ③ at the bottom. Assuming that one of the green frames at the position of the shoulder in step ③ is a black one, one of the yellow and red frames is a white one, and the number of consecutive white cells is 4, which exceeds the specified 3 in problem cell. Therefore, the two cells in the green frame must be white cells.
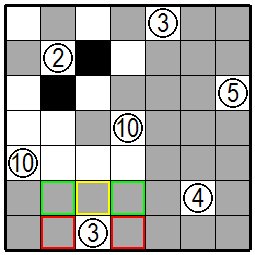
今度は再び左上の②の上の黄色の枠の枡を考えます。この枡が白枡だとすると②からはじまる白枡の連続は２となりますので②の左の緑色の枠の枡は黒枡となります。 すると左上の白枡の塊が黒枡で分断されないためには赤色の枠の枡が白枡にならねばなりませんが、ここが白枡になるとその右にある③の枡から始まる白枡の連続が５になってしまいますので最初の黄色の枠の枡は黒枡でないといけません。 また赤色の枠の枡は白枡でないと黒枡による分断が発生しますので白枡となります。③の枡から始まる白枡の連続も３になりましたので③の右と下は黒枡。中央の⑩の上も黒枡の分断が起きないよう白枡となります。 Now consider again the yellow framed cell above ② in the upper left. If this cell is a white cell, the number of consecutive white cells starting from ② will be 2, so the green frame on the left of ② will be a black cell. Then, in order for the mass of the white cell in the upper left not to be divided by the black cella, the cell in the red frame must be a white cell. Since the continuation will be 5, the first yellow frame must be a black cell. If the red frame is not a white one, it will be divided by a black one, so it will be a white one. The number of white cells starting from the cell in ③ has also become 3, so the right and bottom of ③ are black cell. The top of the central ⑩ will also be a white one so that the black one will not divide board.
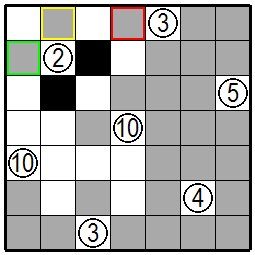
今度は右端の⑤の枡に注目します。この枡の上の緑色の枠の枡は黒枡による分断が起きないように白枡に、左の赤色の枠の枡は白枡になると問題指定の５を越えた白枡の連続になってしまいますので黒枡です。 Now look at the cell ⑤ at the right end. The green frame above this cell is a white cell so that the black cell does not divide board. If the red cell on the left is a white ,the continuos white cell number exceeds the designated number of 5, so it's a black cell.
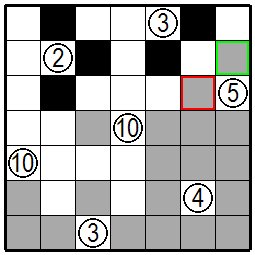
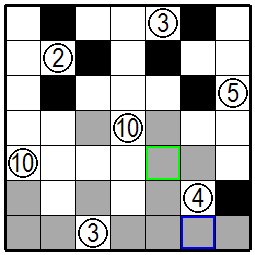
今度は右下にある④に注目します。④の左上の緑色の枠の枡が黒枡だと白枡の連続が４を越えてしまいますのでここは白枡に、④の下の青色の枠の枡が黒枡になるとまだ決まっていない枡をどう白枡にしても白枡の連続が４になりません。でここも白枡となります。 同じように考えていくと右下の正解にたどりつくはずです。 Now look at ④ in the lower right.If the green frame in the upper left of ④ is a black cell, the white cells will exceed four, so here is the white cell. If the cell in the blue frame under ④ becomes a black cell, the white cells will not be 4 even if the white cells are not determined yet, so they are also white cells. If you think in the same way, you should reach the correct solution in the lower figure.

---