1. 盤面の枡のいくつかに縦横に二つ並ばないように黒枡を配置します。 Arrange the black cells so that they do not line up vertically and horizontally in some of the cells on the board.
2. 太い枠線で囲われた長方形の枡のグループに問題数字がある時はそのグループにはその数字と等しい数の黒枡が配置されます。 数字のないグループでは黒枡の数はいくつあっても構いません If there is a problem number in a group of rectangular cells surrounded by a thick border, the same number of black cells will be placed in that group. For groups without numbers, there can be any number of black cells.
3. 縦横に連なった白桝は3グループにわたってはいけません。 White cells connected vertically and horizontally must not span three groups.
4. 黒枡で盤面が分断されてはいけません。(白桝はすべて縦横に繋がります) The board must not be divided by black cells. (All white cells are connected vertically and horizontally.)

へやわけの問題へ jump to Heyawake problem.

---

解くポイントはまず数字のあるグループでグループの形と数字で一意に黒枡位置が決まるところに注目します。例えば1×3のグループで2の指定がある、 3×3のグループで5の指定があるなどです。数字が0のグループも全枡白桝に決まります。
次は辺や角で同じ様にグル－プの形と数字で黒枡が決まるところに注目です。例えば辺にある3×2（辺に接するのは3）で3、角の2×2で2などです。
その後は黒枡の隣枡が白桝に決まったり、黒枡による分断が起きないように白桝に決まったりするところを白桝にします。 するとグループの未定の枡が上の手法で決まる枡が出てきます。
白黒未定の枡をすべて黒枡にすると問題数字の黒枡数になる時も黒枡に決定できます。
あとは白桝が3グループにならないように黒枡にする、黒枡で分断されないように白桝にしていくように進めます。
The point to be solved is to focus on a group with numbers, where the shape of the group and the number determine the position of the black basin uniquely. For example, a 1 × 3 group has 2 designations, a 3 × 3 group has 5 designations, etc. In a group with a number of 0,all cells are also determined as a white cells.
Next, it is noteworthy that the shape of the group and the number determine the black cells in the same way on the sides and corners. For example, a group with problem cell 3 specified by 3 x 2 on the side (3 in contact with the side), a group with problem cell 2 specified by 2 x 2 on the corner, and so on.
After that, the place where the next cell of the black cell is decided to be a white cell or the place where it is decided to be a white cell so as not to be divided by the black cell will be a white cell. Then, there will be a cell whose group is determined by the above method.
If all the black and white undetermined cells are changed to black cells, the number of black cells in the problem figure can be just determined as black cells.
After that, we will make the black cells so that the white cells will not be connected to the three groups, and the white cells so that they are not divided by the black cells.

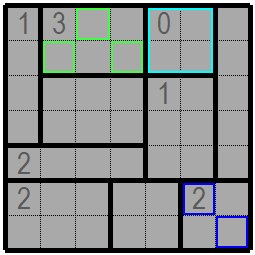
実際の問題で説明します。次の図が問題です。 分かり易くするため白黒未定の枡は灰色表示になっていますが　実際の問題では一般には黒枡と白桝の表示になっています。 Let me explain with a real problem. The following figure is the problem. For easier understanding, black and white undetermined cells are shown in gray, but in practice, black and white cells are generally displayed.
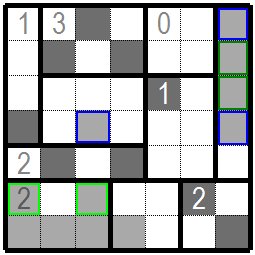
まず右上の水色枠のある0のグループでは全枡白桝に決まります。 また 上左の黄緑色の枠の枡の3×2のグループでは黄緑色枠の枡が黒枡になります。 黄緑枠の枡を白桝にし　残りの枡を黒枡にすると黒枡による分断ができてしまうからです。 右下の青色枠の枡のある2×2の枡では青色枠の枡を黒枡にしないと黒枡による分断がおきます。 グループ指定数の黒枡位置が決まれば同じグループの黒枡以外の枡は白桝になります。 First, in the group of 0 with a light blue frame on the upper right, it is determined as all white celles. In the 3x2 group of the yellow-green frame on the upper left, the yellow-green frame is a black cell. If the yellow-green frame are white cells and the remaining cells are black, the black cells make separate them. In a 2x2 cell with a blue cell at the bottom right, if the cell with the blue cells re not a black cells, it will be divided by the black cells. If the position of the specified number of black cell is determined, the other cell in the same group will be white.
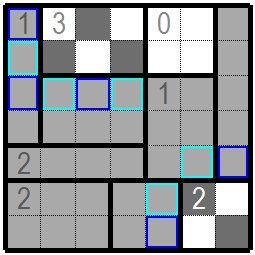
黒枡が決まった枡の隣枡、図では水色枠の枡は白桝になります。 また黒枡による分断が起きないよう青色枠の枡も白桝に決まります。 The cell next to the cell where the black square is determined is white, the cell with the light blue frame is the white cell in this figure . In addition, the blue frame is also determined as the white cell so that the black square does not separate.
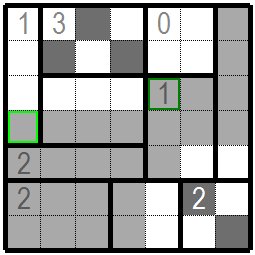
次は左端の黄緑色枠の枡のある数字1のグループを考えます。このグループでは白黒未定の枡がこの黄緑色枠の枡だけです。 この枡を黒枡にしないと指定された　1個の黒枡が配置できませんの黄緑色枠の枡は黒枡になります。黒枡の隣枡は白桝になります。 また緑色枠の枡は黒枡にしないと左側から連続した白桝が3グループ連続になってしまいます。緑色枠の枡が黒枡になれば問題数字指定の黒枡を配置し終えたので同じグループの残りの枡は白枡になります。 Next, consider the group of number 1 with a yellow-green frame at the left end. In this group, the only black-and-white undetermined cell is this with a yellow-green frame. Unless this cell is a black cell, the specified one black cell cannot be placed. The cell with a yellow-green frame is a black cell. The next cell next to the black cell will be a white cell. If the green frame is not a black square, three groups of white cells from the left side will be continuous. If the green frame becomes a black cell, the black cell with the specified problem number has been placed, so the remaining cells in the same group will be white cells.
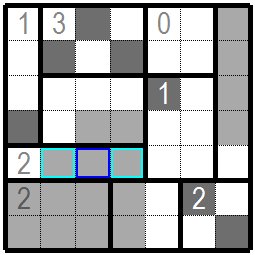
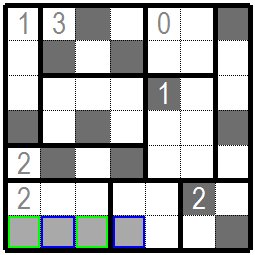
次は水色枠、青色枠のある問題数字2のグループを考えると、左端に白桝が一つ決まったことにより残りの枡がちょうど黒枡二枡入る形になりました。 水色の枠の枡が黒枡になり残った青色枠の枡は白桝になります。黒枡の隣の他の枡も白桝になります。 Next, considering the group of problem number 2 with a light blue frame and a blue frame, one white cell was decided on the left end, so the remaining cells were exactly two black cells. The cells in the light blue frame become black cells and the remaining cells in the blue frame become white cells. Other cells next to the black cell will also be white cells.
白桝が3グループ連続にならないよう青色枠の枡は黒枡になります。 また黒枡による盤面の分断が起きないよう黄緑色枠の枡は白桝なります。 黒枡の隣の緑色枠の枡も白桝になります。 The blue frame is black so that the white cells are not continuous in three groups. The yellow-green frame is a white cell so that the black cells does not separate the board. The green framed cell next to the black cell also becomes a white cell.
左下の問題数字2のグループでは3枡白桝となり残り3枡に二つの黒枡がぴったり入る形になりました。 黄緑色枠の枡が黒枡に、黒枡の隣の青色枠の枡は白桝になります。 In the group of problem number 2 in the lower left, three cells becom white, so two black cells fit in the remaining three cells. The yellow-green frame is a black cell, and the blue frame next to the black cell is a white cell.
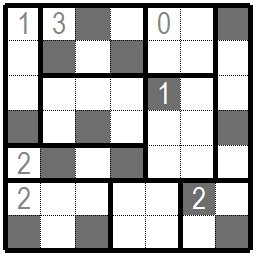
これが正解です。 This is the correct solution.
次は手筋をいくつか紹介します。 まずはグループの形と問題数字から一意に黒枡が決まる例です。辺や角にある時に決まるものも含んでいます。どうして決まるかも考えておくと良いでしょう。 説明のための図ですので解ける問題にはなっていません。 The following are some tips. First, an example where a black cell is uniquely determined from the group shape and the question numbers. Includes what is determined when it is on the side or corner. It is good to consider how it is decided. It is not a solvable problem because it is a diagram for explanation.
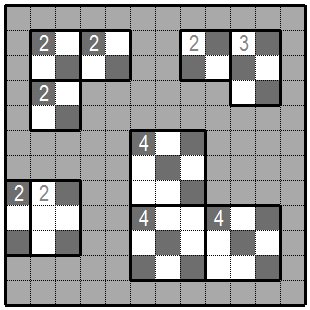
複数のグループの組み合わせで決まるものもあります。 Some are determined by a combination of multiple groups.
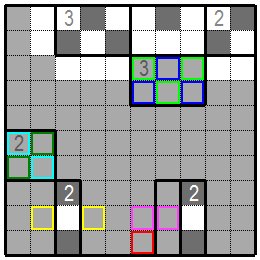
次の図の上部の黄緑色枠と青色枠のあるグループを考えてみます。3個の黒枡を入れようとすると黄緑色枠の三つの枡か、 青色の三つの枡のどちらかですが黄緑色枠の三枡を黒枡にすると黒枡による盤面の分断が起きてしまいます。 従って青色枠の枡が黒枡に、黄緑色枠の枡が白桝になります。 次は左下の部分で考えます。黄色枠の枡はどちらかが黒枡にならないと3グループ連続の白桝となってしまいます。 これを念頭に水色枠と緑色枠のグループを考えると水色枠の枡を黒枡にすると黄色枠のどちらかが黒枡になるため　黒枡による盤面の分断が発生します。 従ってここでは緑色枠の枡が黒枡に、水色枠の枡が白桝となります。 最後に赤色枠の枡を考えます。この枡が黒枡だと桃色枡が白桝となり3グループ連続の白桝となってしまいますので赤色枠の枡は白桝になります。 他にもいろいろのパターンがありますので問題を解きながら覚えていくと良いでしょう。 Consider the group with a yellow-green frame and a blue frame at the top of the following figure. When trying to put three black cells, it is either three cells of yellow-green frame or three cells of blue, but if the yellow-green frame are changed to black, the black cells will break the board. Therefore, a blue frame is a black celland a yellow-green frame is a white celle. Next, consider the lower left part. If one of the cells in the yellow frame does not become a black cell, it will become white cells for three consecutive groups. With this in mind, considering the group of light blue frame and green frame, if the cell of the light blue frame is a black one, then either the yellow frame will be a black one, and the board surface will be divided to two by the black cells. Therefore, here, the green frame is a black cell and the light blue frame is a white cell. Finally, consider the red frame. If this cell is a black cell, the pink cell will be a white cell and become white cells for three consecutive groups, so the red cell will be a white cell. There are various other patterns, so it is better to learn while solving the problem.

---