1. 次の条件に合うように空いている白枡に１～９の数字を入れます。 Fill the empty white cells with numbers 1 to 9 to meet the following conditions.
2. 同一の横一行には問題で与えられている枡を含め 同じ数字は入りません。１～９の数字が1回ずつ入ります。 The same number is not included in the same horizontal line, including the cells given in the problem. Numbers from 1 to 9 enter once.
3. 同一の縦一列にも問題で与えられている枡を含め 同じ数字は入りません。１～９の数字が1回ずつ入ります。 The same number is not included in the same vertical column, including the cell given in the problem. Numbers from 1 to 9 enter once.
4. 太いせんで囲まれた３×３の各ブロックにも問題で与えられている枡を含め 同じ数字は入りません。１～９の数字が1回ずつ入ります。 The same numbers are not included in the 3 × 3 blocks surrounded by thick lines, including the cells given in the question. Numbers from 1 to 9 enter once.
5. 枡の数が全体で25×25の時には使う数字は１～25、ブロックは５×５になります。 同様に全体が16×16なら使う数字は１～16、ブロックは４×４です。他の枡数でも同様です。 When the total number of squares is 25 × 25, the numbers used are 1 to 25, and the blocks are 5 × 5. Similarly, if the whole is 16x16, the numbers to use are 1-16, and the block is 4x4. The same applies to other number of cells.

すうどくの問題へ jump to Sudoku problem.

---

解くポイントは問題で与えられている枡を含め既に確定している枡に注目します。 その数値のある同一横行／縦列／ブロックにはもうその数字は入りません。
ある横行を考えた時には、縦列やブロックからの制限により特定の数字を入れられない場所が在ります。 ある縦列を考えた時には、横行やブロックからの制限により特定の数字を入れられない場所が在ります。 同じようにあるブロックを考えた時には、横行や縦列からの制限により特定の数字を入れられない場所が在ります。
既に確定した同じ数字が2個所あれば両方からその数字が入らない場所を消していくとだんだんと入る場所を限定していけます。 このように限定していってある数字が同一横行／縦列／ブロックの１個所にしか入れられなくなればその枡に確定できます。 The points to be solved focus on the cells already determined, including the cells given in the problem. The same row / column / block with that number no longer contains that number.
Given a row, there are places where certain numbers cannot be entered due to restrictions from columns and blocks. Given a column, there are places where certain numbers cannot be entered due to restrictions from rows or blocks. Similarly, when considering a certain block, there are places where specific numbers cannot be entered due to restrictions from rows and columns.
If there are two places where the same number has already been confirmed, you can gradually limit the places where you can enter by deleting places where the number does not enter from both places. If a number can only be entered in one place in the same row / column / block by these restrictions, it can be confirmed to that cell.

次の図が例題です。ここでは９×９の例ですから　使う数字は１～９です。 太い線で囲まれた３×３の枡がそれぞれブロックです。 分かりやすくするため問題枡は背景を灰色で　太い数字で表しています。 The following figure is an example. Here is an example of 9x9, so the numbers used are 1-9. Each block is a 3x3 square surrounded by thick lines. For simplicity, the background color of the problem cell is gray and thick with numbers.
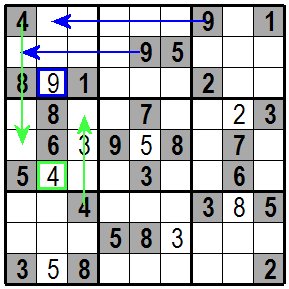
まず左上のブロックに注目します。１行目には右から３枡目に９があり、２行目には左から５枡目に９があります。 従ってこのブロックでは３行目にしか９は入れられませんが３行目で空いている枡は左から二つ目の青色の枠の枡だけですので ９はこの左から二つ目の枡にしか入れられず、この枡の数字が決まります。 同じように緑色の矢印の4に注目すると左端中央のブロックでは緑色枠の枡にしか4は入れられません。 同じように縦列、横行、ブロックの1箇所にしか入れられない数字を入れていくと次図まで解けるはずです。 First look at the upper left block.The first line has 9 in the third cell from the right, and the second line has 9 in the fifth cell from the left. Therefore, in this block, 9 can only be entered in the third row, but the only empty cell in the third row is the cell with the second blue frame from the left. You can only enter 9 in this cell, the number of this cell is determined. Similarly, paying attention to the green arrow 4, in the center block on the left end, only 4 can be inserted in the green framed cell. In the same way, if you enter numbers that can only be entered in one place of columns, rows and blocks, you should be able to solve until the next figure.
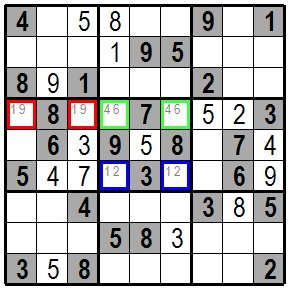
次に一番右側の縦列で上から４枡目の３の下の赤色の枠の枡に入る数字を考えて見ます。 縦の同じ列にある数字(1,3,5,2)、横の同じ行にある数字（6,7,8,9）と同じブロックにある数字（3,6,7）は この枡には入りませんので　結局入る数字は４しかありません。 Next, look at the numbers in the red framed cell below the number 3 in the fourth cell from the top in the rightmost column. The numbers in the same vertical column (1,3,5,2) ,the numbers in the same horizontal row (6,7,8,9) and the numbers in the same block (3,6,7) are not placed on this red framed cell, there is only 4 to enter after all.
新たに書き込まれた数字も使って、上と同じように考えていくと次図まで解けるはずです。(説明のためここで止めてあります。) By using the newly written numbers and thinking in the same way as above, you should be able to solve the following figure.(Stopped here for explanation.)
この例題は今までの繰り返しでも解けますが、違った手筋も考えて見ます。 真ん中のブロックの数字が決まっていない青の枠の枡には1,2,4,6のいずれかが入ります。 この横列には左から２番目に４が、右から２番目に６が既に入っていますので１か２しか入りません。 緑の枠の枡にも1,2,4,6のいずれかが入りますが青の枠の枡に1,2が入りますので　ここには4か6が入ります。 赤い枠の枡を考えると　横一列で残っている数字は1と9しかありませんので1か9が入ります。 難しい問題では候補数字を書き込んでおくと考えやすい時もあります。 You can solve this example by repeating the previous steps, but let's look at a different approach. The blue framed cell in the middle block where the number is not determined contains 1, 2, 4, or 6. This row already contains 4 for the second from the left and 6 for the second from the right, so only 1 or 2 is entered. One of 1,2,4,6 is also entered in the green framed cell, but 1,2 is entered in the blue framed cell, so 4 or 6 is entered here. Considering the red framed cell, there are only 1 and 9 numbers left in a row, so 1 or 9 will be entered. For difficult problems, it is sometimes useful to write down the candidate numbers.
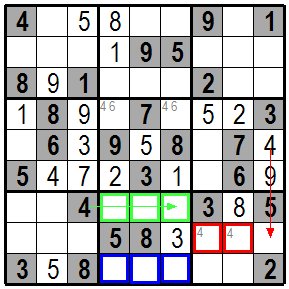
前の図の右側の赤い枠の上には1がありますので9となり、左の赤い枠の枡は1になります。 同じ様に左側の青い枡の上の方には1がありますのでこの枡は2に、右側の青い枠の枡は1になります。 ここでまた違う手筋を考えて見ます。 In the previous figure, there is 1 above the red frameed cell on the right, so it is 9 and the cell in the red framed cell on the left is 1. Similarly, there is 1 above the blue framed cell on the left, so this cell is 2 and the cell with the blue framed cell on the right is 1. Here is another way of thinking.
一番下の段の真ん中のブロックを見てみます。このブロックの真ん中の行は既に5,8,3が入っています。 その上の行の緑色の枠の枡のすぐ左の枡に４が入っていますので緑色の枠の枡に４は入りません。４は一番下の行の空いた青色の枠の枡の いずれかに入ります。右下のブロックを考えると青色の枠の枡のどれかに４が入るので真ん中の行にしか４は入りません。一番右の縦列には上から5番目の枡に ４が入っていますので右端のブロックでは赤い枠の枡のどちらかに４が入ることになります。 Let's look at the middle block at the bottom. The middle row of this block already contains 5,8,3. There is 4 in the cell to the left of the cell in the green frameed cell in the row above it, so 4 does not enter in the green framed cell. 4 goes into one of the open blue framed cell in the bottom row. Considering the block at the bottom right, 4 will be in any of the blue frameed cell, so 4 will only be in the middle row. In the rightmost column, 4 is in the fifth cell from the top, so in the rightmost block, 4 will be in one of the red framed cells.
他にも手筋はありますが、順番に理詰めで数字を埋めていけば最終的には次の図の答えに到達できます。 There are other approaches, but if you fill in the numbers in order, you will eventually reach the answer in the following figure.

---